The excessive trust in fossil fuels has triggered a global environmental crisis, whereby greenhouse gas emissions, air pollution and climate change are intensively associated with the composition of the energy structure. According to the International Energy Agency, the combustion of fossil fuels bears almost 75 % of the global Co.2 Emissions [[1]Present [2]Present [3]]. In this context, the concentration of solar power (CSP) technology (characterized by zero carbon emissions and inherent energy storage function [4]. According to the key components, CSP technologies are mainly divided into four types: tower [5]Parabolic trough [6]Linear Fresnel Reflector [7]and parabolic bowl [8]. Under these, Solarz Power Tower (SPT) systems can use thousands of heliostats to concentrate the solar radiation on a central recipient tower, creating thermal energy with a high temperature to drive steam turbine cycles for power generation [9,10]. In addition to the generation of electricity, tower systems also have considerable potential in providing high -temperature process heat, especially in industrial sectors where temperatures above 900 ° C are required. Recent studies have highlighted this ability. For example, Zolan et al. [11] showed that Solarz Power Tower systems can deliver the heat of the solar industrial process at temperatures up to 1550 ° C at low cost. Nathan et al. [12] Explored the techno-economic feasibility of a solar power tower system to provide process heat at 1100 ° C for industrial applications. Similarly, Alonso et al. [13] showed that tower systems with cavity recipients can achieve cheap energetic and economic performance with increased operating temperatures. These results confirm the technical advantages of tower technologies compared to other CSP systems for high-temperature-related industrial heat applications. With its superior sun concentration and the efficiency of thermal-electric conversion, SPT was recognized as a dominant force in CSP technologies of the next generation [14]Inexpensive and highly efficient design innovations urgently demand.
The thermodynamic border theory with full spectrum usage, which serves as the basis for the SPT system optimization, includes three core elements: heliostat field Optical efficiency limit, recipient-phototothermia conversion efficiency limit and cycle-thermomechanical conversion efficiency limit. In view of the fact that the Heliostat field serves both as the source of the Systems Energy Input and as a primary cost component [15,16]The optical efficiency limit of the Heliostat field not only forms the cornerstone for theoretical research, but also offers the key path for technological breakthroughs.
In existing studies, however, there is no clear understanding of the optical efficiency limit of Heliostat fields and tends to adopt over-idealized assumptions in the construction of theoretical models in order to simplify the heliocyx field into a compact, regular mirror array [17]. The core defect of such a model provides mathematical convenience for the estimate of the optical efficiency limit and, however, lies in its complete neglect of shadow and blocking losses, which are inevitable in practical engineering and theoretically overestimates the calculated optical limit and thus indicates a limited conducting value. More Significantly, While Theoretical Research on the Heliostat Field Optical Efficiency Limin Remains Scarce, Studies Focusing On Optical Efficiency Calculation and Optimization for Specific HELIOSTAT FIELDS – DESPITE THEIR Numerical Predominance – Server Profound Methodological Shortcomings: (I) Strong Empirical Dependency: Existing Studies Either Ignore System Optical Efficiency or Rely on Engineering Experience as References [18–19]without the optical efficiency limit as a theoretical basis; (II) Inadequate theoretical universality: Most studies focus specifically on optimizing the parameter optimization of the Heliostat field. [20] Or layout optimization [[21]Present [22]Present [23]]For heliostat fields in certain regions and scales, especially for the following solid geometric patterns that are easier to optimize [[24]Present [25]Present [26]]. Even if there are positions in which heliostats could be placed to improve optical efficiency, predefined layout rules prevent such a placement. As a result, such designer results have a low universality, and the optimization processes are similar in a similar theoretical basis. These factors limit the further development of SPT systems in the direction of larger standards, higher efficiency and lower costs and urgently require theoretical breakthroughs in this area.
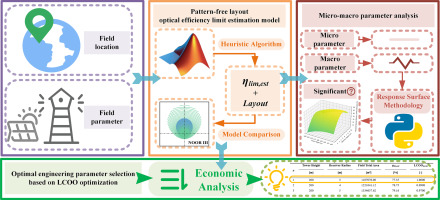
This study deals with the challenges mentioned above by creating a must-free layout layout model for the efficiency limit that achieves double goals: (i) Correction of the optical efficiency limit of overestimation in previous studies by creating an ideal heliocide distance and blocking loss-scene-screening mechanism. (II) Throwing the optical restrictions of conventional, structured heliocide fields via a high-free sample-free layout strategy through elimination of geometric symmetics restrictions to enable the heliocide provision in every spatial position in order to obtain a technically-based benchmark for the realistic optical efficiency limit. The rest of this study is organized as follows: Section 2 contains a detailed introduction to the estimation model for optical efficiency limit proposed in this research, the reaction sober area method (RSM) for parameter analysis and the economic analysis for parameter optimization. In Section 3, the study initially defines the parameter research intervals based on official data. Through a comparative analysis with the existing model, the proposed model shows its ability to reduce the overestimation of the optical efficiency limit, to create the results closer to the technical reality and a basis for subsequent analyzes (Section 3.1). Next, the study uses this model to examine the universal relationships between micro and macroparameters and optical efficiency boundaries in heliocia. Based on the simulation data, the interactions between all macroparameters are specifically analyzed with RSM, which leads to the development of a second order regression model to estimate the optical efficiency limit (Section 3.2). In order to lead the optimal selection of the heliocydrist field parameter combinations, section 3.3 derives the cost-effective optimal parameter combinations using the optical costs (LCOO) and proposes the corresponding optimal roof layout. Section 4 completes the study.